$$ \newcommand{\dps}{\displaystyle} \newcommand{\C}{\mathbb{C}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\N}{\mathbb{N}} \newcommand{\Mf}{\mathcal{M}} %manifold \newcommand{\Lim}{\displaystyle\lim} \newcommand{\ol}{\overline} \renewcommand{\Pr}{\mathbb{P}} \newcommand\diff{\mathop{}\!\mathrm{d}} \newcommand\1{\mathbb{1}} \newcommand\E{\mathbb{E}} \newcommand\Σ{\sum} \newcommand\setX{\mathbf{X}} \newcommand\setY{\mathbf{Y}} \newcommand\inner[2]{\langle #1, #2 \rangle} \DeclarePairedDelimiter\abs{\lvert}{\rvert} \DeclarePairedDelimiter\norm{\|}{\|} \DeclareMathOperator{\softmax}{Softmax} $$

Distances on Markov Chains and their Differentiation

Tristan Brugère

Zhengchao Wan

Yusu Wang

The 35th International Conference on Algorithmic Learning Theory (2024)

1 Introduction

1.1 Introductions

Tristan Brugère
Zhengchao Wan
Yusu Wang

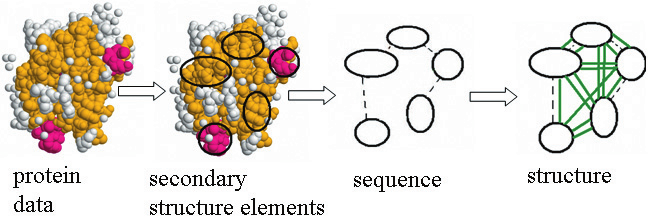
1.2 Motivation: Learning on graphs

A netlist
Protein encoding as graphs

  • (labeled) Graphs are everywhere

    • Chips (directed, labeled, multigraphs)
    • Molecular structures
    • Social networks

  • Discrete or continuous features

  • We want to

    1. Compute statistics on graph datasets;
    2. Make NNs that output graphs

1.3 Problem

\[\text{Loss}(G) = \text{\large\textbf{?}}\]

\[\text{Loss}(G) = d_{\text{graphs}}(G, G_{\text{target}})\]

\[d_{\text{graphs}} = \text{\large\textbf{?}}\]

And we want this loss to be differentiable (for gradient descent).

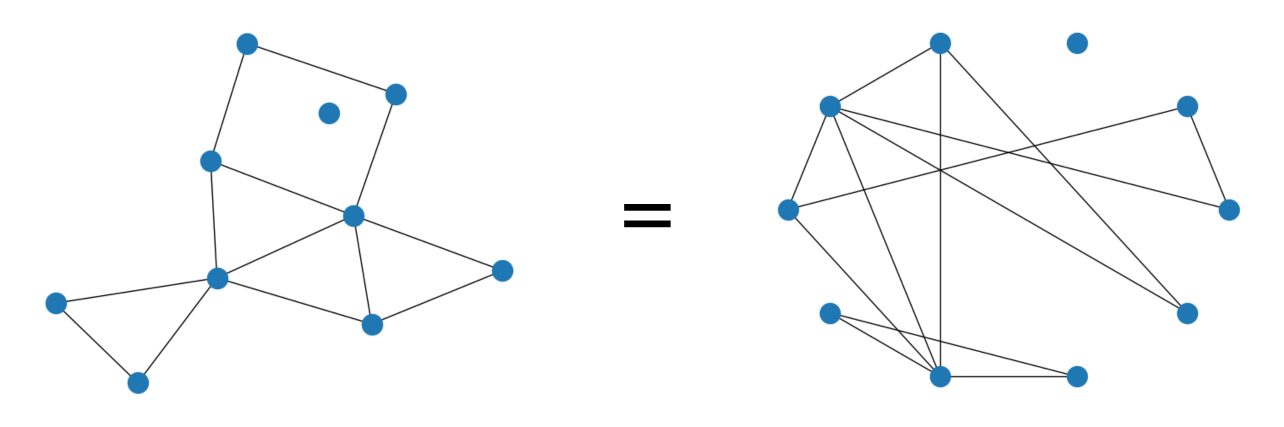
1.4 Comparing graphs is hard

  • Independent of data representation / node ordering
graph isomorphism

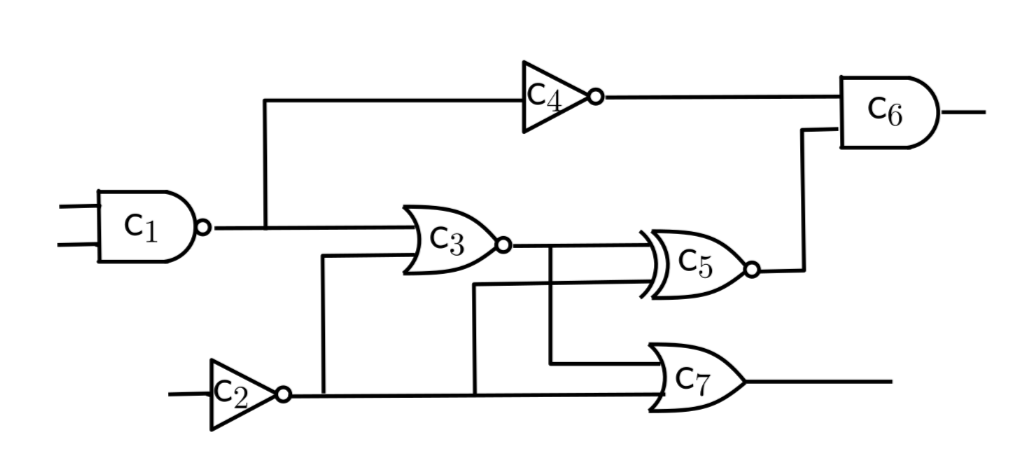
  • No Polynomial algorithm for graph isomorphism

  • Graphs are combinatorial objects (how do we differentiate on the space of graphs?)

1.5 SOTA: FGW

FGW

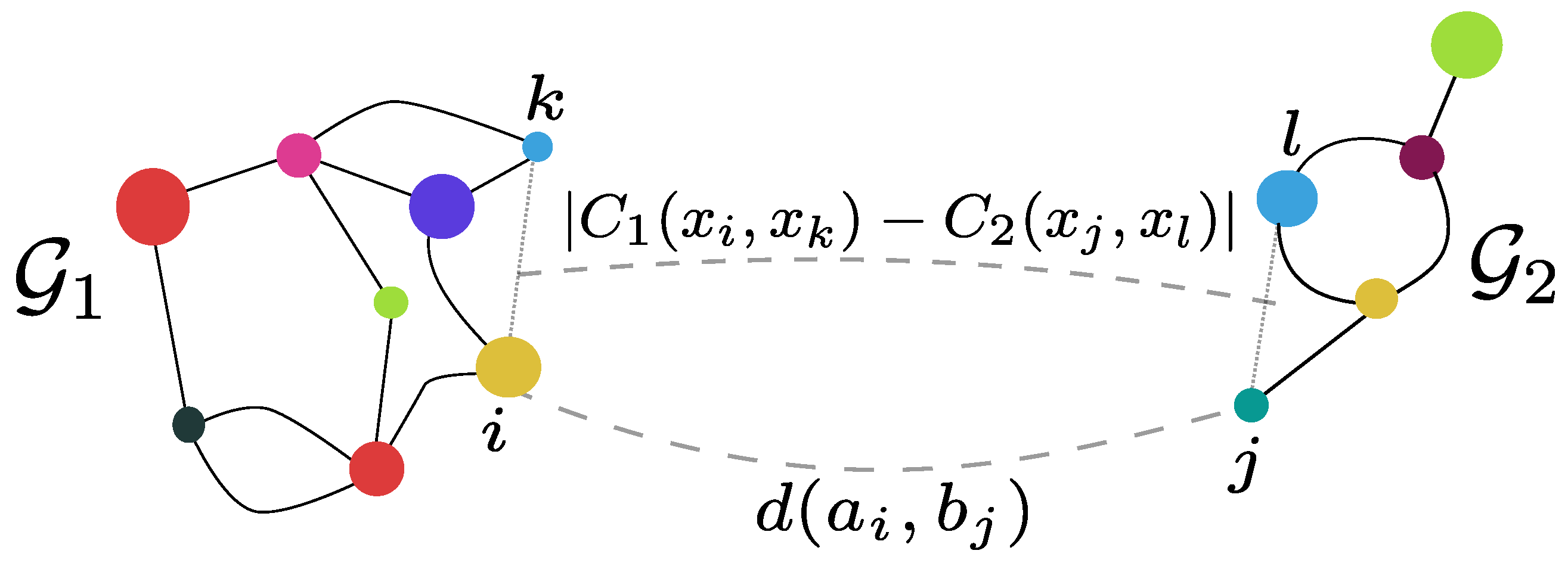
Fused Gromov Wassertein distance (FGW):

  • See graphs as metric spaces

  • Compute a matching of nodes minimizing:

    • Distance between node features;
    • Distortion of the metric structure

1.6 Challenges with FGW:

  • No differentiation
    • (but can be minimized by a heuristic procedure)
  • Computation is heuristic
    • (no guarantee of convergence)
  • Intuition does not apply to directed graphs

1.7 Preliminaries:

A Markov chain with 3 states

  • Markov chain

    • Memoryless random walk
    • On a space of “states”
    • Next state distribution depends only on the current state

  • Optimal Transport (Wasserstein’s distance, Earth mover’s distance…)

    • Compute a soft matching between pointsets
    • minimize that cost

2 Our approach

2.1 From Graph to Markov Chain

\[\text{(labeled) Graph } \simeq \text{ (labeled) Markov Chain}\]

Graph to Markov chain
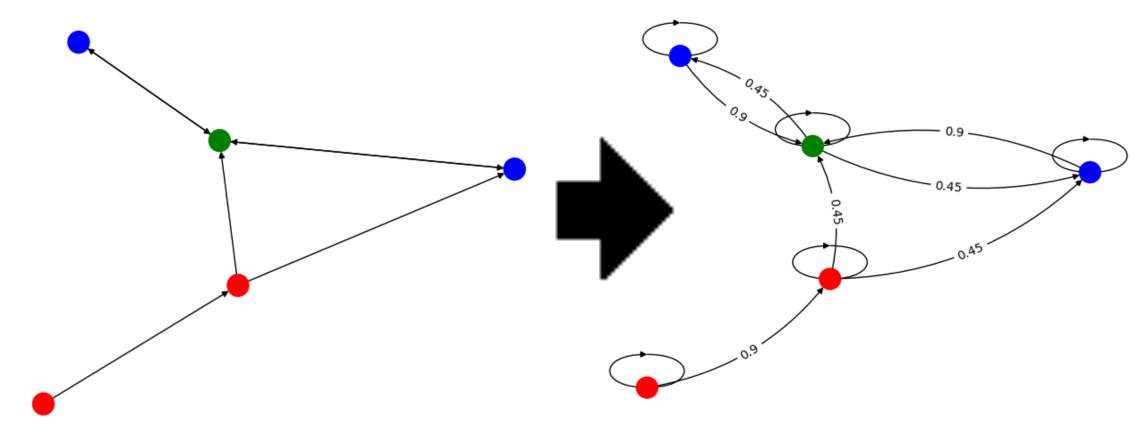
  • Random walk gives a Continuous representation of the combinatiorial object

2.2 Optimal transport on Markov Chains

Regular

Markov

optimal transport For

Pointset law \((p_X, p_X)\)

Markov Chains \((\mathcal{X}, \mathcal{Y})\)

With cost

\(C(X, Y)\) between points

\(C(X_i, Y_i)\) between states

Take \(p\) distribution over \(\N\) and \(T \sim p\) independent of \(X\) and \(Y\)

\[d_{OT}(p_X, p_Y; C) = \inf_{\substack{(X, Y) \text{ coupling} \\ X\sim p_X \\ Y\sim p_Y}} \E\, C(X,Y)\]

\[d_{???}(\mathcal{X}, \mathcal{Y}; C) = \inf_{\substack{(X_t, Y_t) {\color{#D462AD}\text{ Markovian coupling } }\\ X_t\sim \mathcal{X} \\ Y_t \sim \mathcal{Y}}} \E\, C(X_{\color{#D462AD} t},Y_{\color{#D462AD} t})\]

\[d_{\color{#6E963B}OTM}(\mathcal{X}, \mathcal{Y}; C) = \inf_{\substack{(X_t, Y_t) {\color{#D462AD}\text{ Markovian coupling } }\\ X_t\sim \mathcal{X} \\ Y_t \sim \mathcal{Y}}} \E\, C(X_{\color{#6E963B} T},Y_{\color{#6E963B} T})\]

2.3 Contributions: Theoretical Framework

  • Study of optimal transport method for Markov chains

  • Theoretical framework: Optimal transport Markov (OTM) distances.

    • links previous Optimal transport-based methods on Markov chains.
    • (Moulos 2021)
    • (O’Connor et al. 2021)
    • (Chen et al. 2022)

2.4 Contributions: DDWL-Distance

particular case of interest: \(\delta\)-discounted WL distances.

  • Differentiable

    • In the label values and the Markov chain structure
    • With some regularization

  • Computationally tractable

    • converging iterative algorithm

  • Naturally adapted to directed graphs

  • Can work with non-stationary Markov chains

    • adds stability over previous Markov-based methods

2.5 Intuition

  • Similar to the Weisfeiler-Lehman isomorphism test

  • Or to an MPNN

  • “Propagate” labels from neighbors to neighbors (random walk)

  • Determine “how different” the label distributions are

2.6 Formalization

Full formalization: https://tristan.bruge.re/ot_markov_distances/paper

2.7 Experiment: noisy circle barycenter

Compute by gradient descent: \[\text{Barycenter}(G_1, G_2, \dots, G_n) = \inf_{G} \sum d(G, G_i)^2\]

Example noisy graph (ER noise, p=0.01)
Barycenter computed by our distance on 50 such graphs
Barycenter computed by baseline (FGW) on 50 such graphs (non-oriented)

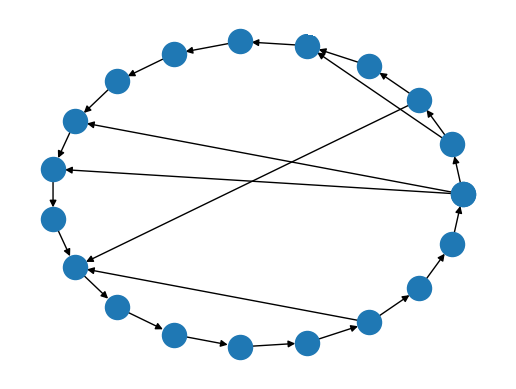
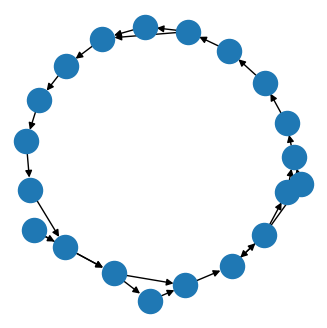
Example output of the barycenter experiment on circle graphs with Erdős–Rényi noise

2.8 Experiment: Synthetic data — noisy circle barycenter (II)

3 Conclusion

3.1 Current challenges and future work

  • Computationally expensive

  • Ongoing work on generative models

3.2 Thank you!

3.2.1 Code

Github link

$ pip install ot_markov_distances

3.2.2 Contact

tbrugere@ucsd.edu

3.2.3 Acknowledgements

This work is partially supported by NSF under grants CCF-2112665, CCF-2217058, and CCF-2310411.

References

Chen, Samantha, Sunhyuk Lim, Facundo Mémoli, Zhengchao Wan, and Yusu Wang. 2022. “Weisfeiler-Lehman Meets Gromov-Wasserstein.” In International Conference on Machine Learning (ICML), 3371–3416. PMLR.
Moulos, Vrettos. 2021. “Bicausal Optimal Transport for Markov Chains via Dynamic Programming.” In 2021 IEEE International Symposium on Information Theory (ISIT), 1688–93. IEEE.
O’Connor, Kevin, Bongsoo Yi, Kevin McGoff, and Andrew B. Nobel. 2021. “Graph Optimal Transport with Transition Couplings of Random Walks.” arXiv. https://doi.org/10.48550/arXiv.2106.07106.